NATURE'S NUMBERS

Please watch "All watched over by machines of loving grace:The use and abuse of vegetational concepts"

Mathematics is perhaps not the first subject that springs to mind when thinking of nature,but many modern researchers have endeavoured to explain nature in mathematical terms, and some inroads have been made. There are certain areas of mathematics that impact upon various aspects of nature. In particular,the following areas are worthy of note:

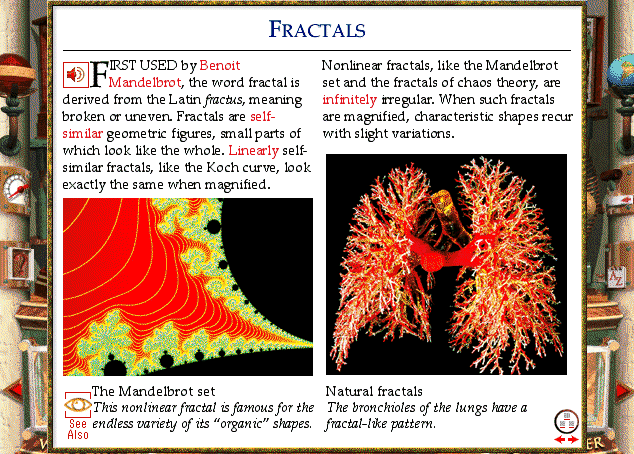
• Fractals - A term contracted from the words 'Fraction' and 'Dimensional'. Fractals explain why some systems in nature are 'self similar',such as ferns.
• The Butterfly Effect & Strange Attractors - This type of mathematics gives us clues about the flow of water and the nature of the weather system.
• Affine Transformations - The processes of reflection,rotation and scaling are seen to be operating in nature to generate biological forms.
• Geometry & Symmetry - Basic geometrical figures can be found in nature,such as the hexagonal arrangement of a snow flake.
• Spirals - Mathematical spirals are seen to occur naturally in snail shells, nautilus, galaxies and in DNA.
• Fibonacci Numbers & The Golden Ratio - Number series can indicate the pattern of growth in rabbit populations and terms may be found in the number of petals of a flower.
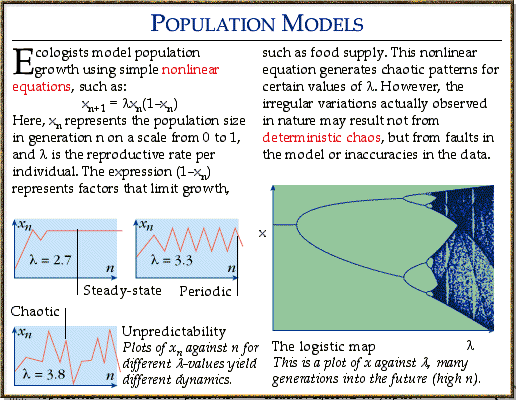
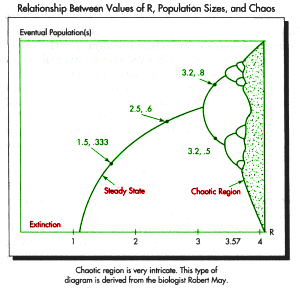
• Population Dynamics - Certain areas of maths such as differential calculus can be shown to govern how populations grow and collapse.
• Animal Skin markings - The mathematics of 'Reaction Diffusion' can explain the patterns on animal skins.

	Fractals - In our world we are used to measuring things in the three dimensions of length, width and depth. Some of the things we find in nature do not sucumb easily to such measurements and we are forced to explain their shape using fractional dimensions. Mountain landscapes are a good example of  a fractal, as, if we use a one metre rule to measure around a mountain surface we would miss out all the gaps less than a metre in lengh. If we then used a shorter rule to measure the surface we would find that it would fit in all the gaps and we would end up measuring a longer distance. Fractals are also representative of those types of structure which exhibit "self similarity". In the case of a mountain face,it is made up of smaller and smaller rocks which are vaguely similar.
A better example of such self similarity in nature is a fern, which can readily be seen to be made up of what appear to be copies of itself at smaller and smaller scales. Cauliflower heads and Broccoli also exhibit patterns where copies of a main pattern appear at smaller and smaller scales. Benoit Mandelbrot discovered fractals whilst working for IBM and now has a set of numbers named after him.

The Butterly Effect - The butterfly effect is the propensity of any dynamic system to be sensitive to initial conditions. This type of mathematics pertains to such things as water flow and weather systems, where any slight change in one circumstance can radically alter the outcome. It may also be that our current interaction with the Earth's environment is having a more and more pronounced effect upon the weather system and habitats, as we find that more and more creatures struggle to find a niche in which they can continue to survive.

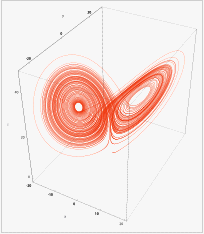
The symbolic representation of this effect is engendered by the Lorenz Attractor, a diagram which is the result of modelling weather equations. Such equations exist for many natural processes, including fluid flow. The diagrams which represent the equations are called "strange attractors" after their propensity to try and keep the variables in the equations within certain extremes. In the case of the Lorenz attractor,the red lines indicate normal weather patterns,and the other areas may be the points that we don't normally see such as snow in the desert. Such attractors are behind modern computing methods used to give us weather predictions and can also be used to predict catastrophes such as volcano eruptions and earthquakes.

Affine Transformations - These are the processes of rotation, reflection and scaling. Many plant forms utilise these processes to generate their structure. In the case of Broccoli and Cauliflower heads, it can readily be seen that there is a type of pattern, which also shows some spiralling in the case of Broccoli.
It is perhaps not so obvious what is happening in a Cauliflower head, but perhaps the process of taking a smaller copy and rotating it is very evident in the case of a fern, where each branch appears to be a smaller version of the main plant and so on, at smaller scales.
The branching processes of trees which do not appear to the naked eye as self similar can also be modelled with branching computer programs called L-systems which attempt to understand the structure of trees in terms of branching rules.

	Symmetry - It is obvious to us as human beings when we look in the mirror that to a large degree our own bodies have an axis of symmetry and that the left and right hand side of us are, to within a degree of error, mirror images of each other. Elsewhere in nature we can see other such symmetries. The most obvious is the six-fold symmetry of a snowflake crystal. The same symmetry can be found in the combs of the social insects such as bees.
Many fruiting bodies such as tomatoes or apples have rotational symmetries or carry segments such as those of an orange which break the circle up into fractional parts. The propensity of symmetries and geometries to show up in natural objects can sometimes be traced to the molecules that make up the object, or possibly because the arrangement of matter takes up the least space or minimises the use of energy,or maximises the use of space whilst creating structural strength.
	The arrangement of atoms in a molecule is not visible to us under ordinary every day circumstamces, but often the properties of any compound can be due to the geometrical arrangment of the atoms in the substance. Water molecules are composed of Hydrogen and Oxygen atoms in the molecule H2O which has configurations of the atoms that may give rise to the hexagonal structure of the snowflake.
It is worth noting that some molecules come in left and right-handed versions which are called Chiral molecules and before the human race new of the consequences of  this simple reflection, it was assumed that the
variation in the molecules symmetry made no difference to the chemical properties of the actual molecule. In fact, we now know that it very much does affect the properties,and in at least one case, lack of knowledge of Chiral molecules led to a medical travesty,that of Thalidomide. Chiral molecules are also at large,where there is a variation in taste,such as lemon and orange fruit.

Spirals - The most well-known, if little actually witnessed spiral in nature is our own DNA inside our cells, this of course is known as the "double-helix" and a helix is slightly different than a spiral, but as with the above geometry it is interesting that there are subtle mathematical relationships between the atomic arrangment of molecules and the symmetries of the forms that those molecules are involved in creating.
	Another, more readily observed spiral in nature, is the arrangement of the outer skin of a Pineapple. On this fruiting body, we can see two interlacing spirals wrapped around the surface of the fruit. We can see a similar arrangement in the seeds of the seed-head of the sunflower,and we also find that such spirals are sometimes a consequence of Fibonacci number sequences and an attempt by the flower or fruit to maximise the number of seeds into the space that it has for them.
More common spirals in nature appear in snail shells and a particularly beautiful example is the shell of the Nautilus, whose flotation chambers are arranged in a mathematical sequence of increasing size as the animal grows within it's shell. We might see from this that the shell shape is a consequence of the process of increasing size of the contained animal and that the shape is not 'designed'.
Spiral galaxy  - a consequence of the physical laws of gravitation.		Further out into the cosmos we still find spirals, and so we can see that mathematics is at large in our universe, from the very smallest scales of the atom right up to the largest scales that the universe can provide.

Fibonacci Numbers - Fibonacci numbers are those that create a sequence, by adding up successive numbers starting with 1 which is added to itself to get 2, then 2 is added to 1 to get 3 and then 3 is added to 2 to get 5 and so on. This sequence - which continues 8,13,21... -very often is behind the arrangement or number of petals in a flower head or the number of seeds or spirals in a fruiting body.
	Because it is a relatively simple sequence where the next term is generated from the previous one, it is something plants can do easily, and also easy for computers to copy. Such sequences can also be behind the spiralling arrangements often seen in biological forms. If we lay the terms out on a two-dimensional diagram,we can generate spirals.
Above: A cross-section through a bamboo with a hexagonal outer edge,and right, the seed arrangement of pine cones. Below: The seed head of a sunflower.		Pine cones are another good example of where we see spirals and Fibonacci numbers,as with the Pineapple, the pattern  is obvious to the eye, but without a mathematical understanding we take these aspects of nature for granted or attribute them to a 'designer'.
	The terms of the Fibonacci sequence are also present in the reproduction rates of rabbits, which may account for the surprising increase in the populations of them, so much so, that they are often used as a symbol of fertility as when Easter cards carry images of them. Population growth and dynamics is another area of nature that mathematics has rather a lot of impact upon.

Population Dynamics - This area of mathematics is sometimes controversial because it starts to make statements about policies such as culling and vaccination,which people often create emotional arguments about without understanding the facts, or possibly go looking for causes which don't actually exist. Currently,for instance, the human race is witnessing a collapse in the population of bees and is also concerned about over-fishing. There have also been arguments about seal culling, whaling and also the hunting of foxes. In the public domain, very few people are aware of the work that has been done analysing how populations of creatures grow and develop and sometimes collapse. In particular, the work of Robert May on Chaos Theory as it applies to populations has shed some sometimes counter-intuitive light on population dynamics. There are some computer models which capture some of the essences of either populations of creatures or cellular systems. John Conway's LIFE program attempts to mimic the way a cell culture might grow or display characteristics or even die off altogether. 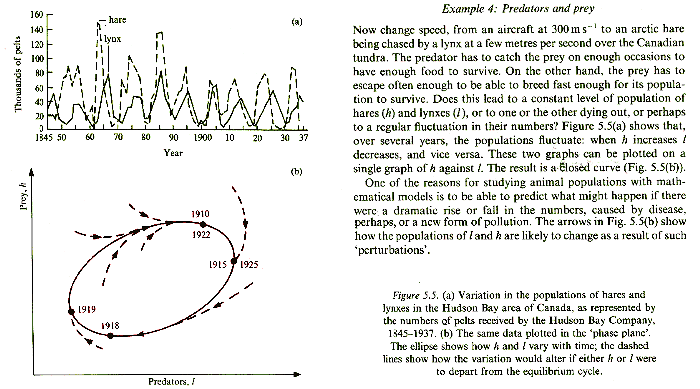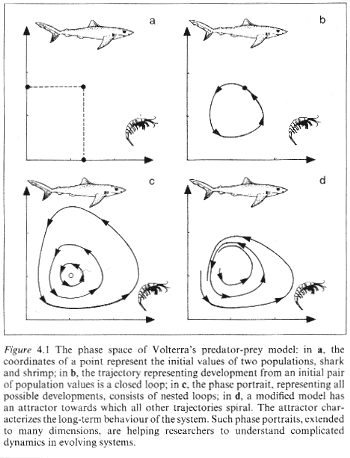Most interestingly - the program only has 3 rules and yet exhibits complex behaviour - including reproduction and evolution and mutation. Cells in his program can proliferate or die depending in what environment they start off and it maybe we have lessons to learn about cause and effect in the environment - if we see that the dinosaur population crashed - we go looking for a meteor crash site or a virus or an environmental change. Mathematical models tell us that this need not be the case,and also instruct us that we might think we can keep fishing and fishing with given "quotas" and feel safe in doing so - but it may not in fact be the case. Those of the country set seem to think they understand how to control 'pests' such as foxes or maybe even squirrels, but the populations are subject to factors such as availability of food and the propensity of pedators to kill them - all of this must be taken into account before a crass 'cull' is taken up,for we may actually be shooting ourselves in the foot when we discover a knock-on effect,or indeed Butterfly Effect because of unseen conequences of our actions. Simple predator-prey modelling is done using differential calculus and can easily be watched on a home computer,it becomes apparent when doing so that simple meddling with a population with a cull is ill-advised and it behoves us as humans to understand the complexity of population dynamics before trying to exhibit control over it.

The following is an extract from "A Mathematician Reads the Newspaper" by John Allen Paulos

Rodent Population Patterns Difficult to Fathom Ecology, Chaos, and the News News stories on ecological issues always seem to be on the verge of making what philosophers used to call a category.mistake, describing a situation as if it belonged to one logical type or category when in fact it belongs to another. In the case of ecology, there is a tendency to look primarily for culpability and conflicts of human will rather than at the dynamics of a natural process. (I'm reminded of the comedian who announced that an Iranian terrorist group had claimed responsibility for the 1993 floods in the Midwest.) Often, however, there are no discernible agents, no Whos to write about. Furthermore, the process isn't instantaneous or precisely localized, so the journalistic When and Where seem inappropriate as well. Moreover, the What, Why, and How are generally complex and impersonal, often beyond the complexity horizons of most readers and sometimes even of the ecologists themselves. An intriguingly simple ecological example studied by the biologist Robert May and the physicist Mitchell Feigenbaum illustrates. Imagine that the population of a certain animal species is given by the so-called logistic formula X' = RX(1-X), where X is the population one year, X' the population the next year, and R a parameter that varies between 0 and 4. For simplicity, we take X and X' to be numbers between 0 and 1, the true population being, say, 1,000,000 times these values. If we assume the population X is now .1 (that is, 100,000) and R = 1.5, we can calculate the population next year, X', by plugging .1 into the formula, obtaining 1.5(.1)(.9), or .135. To calculate the population for two years from now, we plug .135 into the formula and obtain 1.5(.135)(.865), or approximately .1752. If you have a calculator handy, you might want to verity (or you might not) that the population for three years from now will be .21676. I'll spare you any more arithmetic, but the same procedure may be used to find the population for any future year. You would find that the population grows rapidly and then stabilizes at .3333. Moreover, you would find that whatever its original value, big or small, the population would still stabilize at .3333. This population is termed the steady state population for this value of R (see diagram). If we perform similar calculations for a smaller R, say, R = 1, we find that whatever its initial value, the population "stabilizes" at 0; it becomes extinct. When R is bigger-2.5, to be specific-we find in carrying out these procedures that whatever its initial value, the population now stabilizes at approximately .6, the steady state for this R. So what? Well, let's increase R a little more, this time to 3.2. As before, the original population does not matter, but now when we substitute iteratively into the formula X' = 3.2X(1-X), we find that the population of the species doesn't stabilize at one value, but eventually settles into a repetitive alternation between two values: approximately .5 and .8; that is, one year the population is .5 and the next it's .8. Let's raise our parameter R to 3.5 and see what happens. The initial population is once again immaterial, but this time in the long run we have the population alternating regularly among four different values, approximately .38, .83, .50, and .88, in successive years. If we again increase R slightly, the population settles down to a regular alternation among eight different values. Smaller and smaller increases in R lead to more doublings of the number of values. Then suddenly at approximately R = 3.57, the number of values grows to infinity and the population of the species varies randomly from year to year. This is an odd sort of randomness, however, since it results from iterating the formula 3.57X(1-X), and the sequence of populations is thus quite determined by the initial population.) Even stranger than this chaotic variation in the species' population is the fact that a slight increase in R again results in a regular alternation of the species' population from year to year, and a further increase again leads to chaotic variation. These orderly alternations followed by random chaos followed again by windows of regularity are critically dependent on the parameter R, which seems to be a gross measure of the volatility of the model. A close-up view of the chaotic region reveals an unexpected intricacy, and, as in the case of the economy discussed earlier, there is a lesson to this intricacy. If a system as trivial as this single nonlinear equation can demonstrate this sort of chaotic unpredictability, perhaps we shouldn't be quite as assertive and dogmatic about the predicted effects of various ecologic policies on the gigantic nonlinear system that is Planet Earth. The policies' consequences, one would think are considerably more opaque than are those of the value of R in this model. Let me reiterate that there are no agents involved in the story; no greedy corporate despoilers or overzealous environmentalists. Any news story that purported to explain the variation in population would either have to attribute it falsely to someone or something comprehensible to most readers or else find some other way to present the account. As in reporting on the economy and other complex systems, there is a tendency to settle upon some stylized, conventional set of stories that focus on turf and clout rather than on the intricacies of the impersonal system in question.

Animal Skin markings - When we look at a Leopard's spots or the markings of a Dalmation,or maybe even the wing's of a Butterfly,we maybe apt to think that these patterns are intrinsically random or perhaps entirely a property created genetically via evolution perhaps to enable a species to survive by creating a warning sign or by echoing some aspect of the environment for camouflage purposes.
	What may not be apparent is that work done by Alan Turing suggested ways in which maths might explain such markings, but latterly we have begun to understand the patterning on animals in terms of Reaction Diffusion equations. These can produce stable states which may offer a glimpse as to how chemical systems in a biological system work to create a pattern.
Such systems are equally capable of producing rings such as those seen on certain species of butterfly, so when we look at the nature around us, it might be worthwhile considering the phrase "I never did maths at school, I didn't see what I would use it for"!!

How did the leopard get its spots?

LifeSonia Van Gilder Cooke, reporter Rudyard Kipling was half-right, say William Allen and colleagues of the University of Bristol, UK. The team googled pictures of big cats and matched their coats to computer-generated patterns. The resulting classification was used to test the relationship between a cat's patterning, where it lives, and how it hunts. The researchers found that nocturnal tree-dwellers have evolved complex coats to match a dappled, dark forest, while cats stalking the open plains tended to be more plain. One exception is the cheetah, whose patterned coat contrasts with its monochromatic hunting grounds. Allen said this might be explained by the cheetah's hunting strategy, which relies not on camouflage, but on speed. Low genetic diversity might also be a cause. "It may be that there isn't variety in the population to become anything other than spotted," says Allen. For other cats, however, camouflage evolves in response to environment over short periods of time, suggesting a leopard can actually change its spots. Allen drew inspiration for the title of his study from Rudyard Kipling's Just So Stories. "Rudyard Kipling was wrong by suggesting how leopards got their spots as the fingerprints of a man," Allen told the Telegraph. "But he was right about the reason because they provide the perfect camouflage in a forest habitat with dappled light." Journal reference: Proceedings of the Royal Society B, DOI: 10.1098/rspb.2010.1734

Natural food fractals - Cauliflower and Broccoli

Related Videos
	Natural Fractals
	Fractal Landscape Flyby
	Affine Fern
	Tree Fractal
	L-system apple tree
	Nature by Numbers

Further Reading
	Nature's Numbers - Ian Stewart [ISBN  0-297-81642]
	Nature's Chaos - James Gleick & Eliot Porter [ISBN 0-7474-0759-2]
	New Applications of Mathematics - Christine Bondi [Chapter 7]

Images from Oaken Clough Garden
	The segments of this plant reduce by the same amount in length in each segment.
	A fern - an example of natural fractal.
	A fern unfolds from a spiral.
	Example of Pentagonal symmetry, natural spiralling and affine transformation. Click on a plant below to see it's symmetry.